Kolb’s experiential learning theory and its application in the mathematics teaching in third grade
Maria Petrova TemnikovaTrakia University Faculty of Education, Stara Zagora |
|
Teaching methodologies of particular subjects |
Number of the paper: 63 |
Professional paper |
Abstract |
|
The improvement of the efficacy of the pedagogical interaction during mathematics classes in Grade 1-4 is not only connected to the choice of strategies, technology, and methods of work of the teacher, but also to the learning styles used for acquiring the abstract educational content. The article covers different theoretical concepts related to the theory of studying through experience by Kolb who introduces four different cognitive styles of learning; problem production strategies of education and the problem-solving process. The paper presents specifics of researched methodical variants of work with different text tasks where solving involves Kolb’s experiential theory which can be applied in the education in mathematics in primary school. In the research work, reproduction and problem productive methods are applied such as problem exposition, heuristic, research and situational method, discussion, problem-solving discourse, solving of problematic tasks by analogy, and others. In respect of the results from the empiric research, mathematical-statistical methods are used for data processing. In the course of the empiric research two tests were applied: one for the determination of entry diagnostic and the other, after applying the new methodology system of work - for exit diagnostic of the knowledge, skills, and competencies of the Grade 3 students to solve text tasks. As a result of the applied new methodology system of work conditions for the four cognitive styles of learning were created which ensured the development of the knowledge and skills of the students to solve text tasks on a higher level. |
|
Key words |
|
cognitive styles of learning; mathematical text task; problem-productive strategy |
Introduction
The modernization of the education in mathematics for a primary school in Bulgaria is a long and complicated process and is related to the replacement of one educational paradigm with another. Changes covered the state educational policies, the program systems, the educational programs in mathematics, the educational content, the approaches, the methods, and techniques for effective education. To achieve the educational goals, tasks and expected results specified by the state educational requirements as well as to realize active subject-subject interrelation during mathematics classes in Grade 3, of great importance are both the strategies, and the technologies applied by the teacher and the knowledge of the learning style of the students.
If the teacher is familiar with the learning style of the students from the age of 7-11 years, then he will be able to recognize its strong sides. In this way, he will have the chance to apply suitable methods in order to compensate for its weak sides thus assuring higher efficiency of the learning process. Consequently, this facilitates the process of forming skills in the students to show flexibility and to apply their knowledge in non-standard conditions during solving creative mathematical text tasks. The basis for development by the teachers of efficient strategies for teaching and learning the educational content in mathematics is the recognition of the individual learning style of the students. According to Fielding (Fielding, 1994), the inconsistency between the learning style of the student and the teaching approach adopted by the teacher will have a highly negative effect on the overall learning process.
After analyzing foreign and Bulgarian publications, it was found that there are different developed models of learning styles. “More than 70 theories related to the learning style are known.” (Felder, 1996, pp. 18-23) Among them are those of Corno and Snow (1985), Entwistle (1981, 1991), Entwistle and Ramsden (1983), Griggs (1991), Hudson (1966), Pask (1976), Riding (1997), Riding and Chema (1991), Witkin et al. (1977), etc. The learning styles are also studied in Bulgarian sources including the related cognitive styles: Doncheva (2017), Ivanov (2004), Krumova (2018), Lecheva (2009), etc.
One of the definitions of a learning style belongs to the NASSP (the National Agency of Secondary School managers in the USA) which states that: “the learning style is a composition of cognitive, affective and psychological characteristics which are relatively stable indicators of how the student perceives, interacts with and responds to the educational environments.” (Grigss, 1991, p. 2) There must be a differentiation between the cognitive learning style and the learning styles in general as the first concept has a narrower scope.
Some researchers like Griggs (1991), Keefe (1979), and Riding and Chema (1991) include problem-solving in the characteristics of the cognitive learning style. According to Keefe (Keefe, 1979, pp. 1–17), the cognitive style is “the typical way for processing of information by a person – perception, thinking, memory and problem-solving.” For Riding and Chema (Riding, Chema, 1991) this style is the normal approach to problem-solving, thinking, perception, and memorizing of information.
The purpose of the research work is to outline the main characteristics of Kolb’s experiential learning theory and to describe some of the ways of its application during the education in mathematics in Grade 3 for solving text tasks.
Literature review
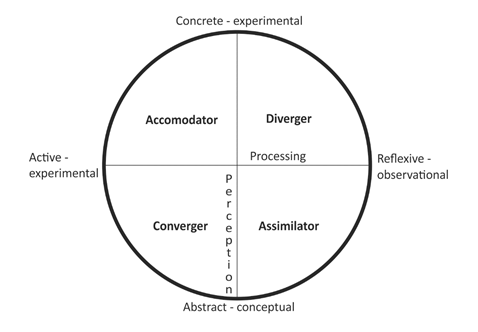
For the purposes of developing the model of experiential learning Kolb steps on the research works of Jung, Dewey, Lewin, and Piaget. According to Fielding (Fielding, 1994, p. 395), “he goes beyond the bipolar approach of Witkin, Hudson, and Pask and argues for a fourfold model which incorporates differences in the ways individuals perceive or grasp the nature of experience and then process or transform it.” Kolb (Kolb, 1984, p. 38) summarized that „learning is the process whereby knowledge is created through the transformation of experience.“ An important feature of his theory is the conclusion that learning is a cyclic process. The stages follow one after the other in sequence – concrete experience (CE), reflexive observation (RO), abstract conceptualization (AC), and active experimenting (AE) – and the students must systematically go through them.
Behind the concept of cycle “lay two primary axes: an abstract conceptualization-concrete experience (AC-CE) dimension and an active experimentation-reflective observation (AE-RO) dimension. These reflect the two main dimensions of the learning process that correspond to two major ways by which we learn. The first is how we perceive or grasp new information or experience, and the second is how we process or transform what we perceive.” (Healey, Jenkins, 2000, p. 187)
Kolb’s cycle includes four stages related to different learning styles that reflect students’ preferences in the way they receive and process information. The learning styles identified by him are related to different approaches for problem-solving which are embedded in every text task from the education in mathematics in Grade 3.
Healey and Jenkins (2000) adapted the characteristics of Kolb's learning styles outlined by Kolb (Kolb, 1984, p. 86) and Gibbs (Gibbs, 1988, p. 20) and consider the effect which they have on the education in geography in Universities.
Ivanov (Ivanov, 2004, p.30) wrote that “divergers are students who perceive concrete information and reflectively process it and also they need to be personally engaged in the cognitive activity. Convergers are students who perceive abstract information and reflectively process it. They also perform detailed, consistent steps in thinking and learning. Assimilators are those students who perceive abstract information and actively process it. They need to be drawn to pragmatic solutions to cognitive problems. Accommodators are students who perceive concrete information and actively process it. They must be drawn into risky, experimental, and flexible cognitive activities.”
According to Kolb (1984), the following types of students were specified – concrete-experimental, reflective-observational, abstract-conceptual, and active-experimental.
Figure 1. Type of students and learning styles according to Kolb
Mihova (Mihova, 2002, p. 79) described the four learning styles: “Accommodative style (accommodators): а combination between concrete-practical and active-experimental styles. The representatives of this style have the ability to learn directly from experience … and do not refuse to be included in new and unknown educational situations. They are able to search for the meaningful and the important in the educational experiment, consider the options on how to proceed, and take into account what others have done in this situation before them. They deal well with complex problems and are able to see the relationship between given components. This type of student prefers indirect strategies for education which enables them to take the role of researchers and knowledge seekers.”
In the problem-solving process, they rely more on other people than on their own analysis. The teachers who work with such students shall use various methods of education but must always keep in mind that the accommodators want to be active participants in the educational process.
Assimilative style (abstract conceptualization, reflexive-observational). This is a style based on logic, a combination of abstract-conceptual and reflexive-observational styles. This type of student has preferences for the exact and logically presented information and not its practical value. The random and aimless studying of problems for them is a waste of educational time. They require the teacher to be an expert and prefer the educational information to be visualized by demonstrations. These students are the least provocative to the teacher. They tend to follow punctually the teacher if he is approachable and able to answer their questions.
Divergent style (concrete experience, reflexive observation). This style is a combination of the concrete-experimental and the reflexive-observational types. The students who have this learning style prefer to think about a concrete situation and understand what this situation offers them. They would like to receive information in well systematized and structured form. The children are interested in how and to what extent the knowledge they receive is related to their experience and personal interests. This type of student is very good at studying a particular situation from different angles. Their approach to the situation is to do more observation than taking an action. They identify the problems, see new ways of doing the things, and new and creative solutions to the problems. They have an overall view of a situation and present their ideas in an innovative and artistic way. The teacher must actively communicate with the students, answer their questions, and dive into proposals. It will be good to use manuals, recommendations, instructions, and abstracts. Flexible and varied thinking is recommendable.
Convergent style (abstract conceptualization, active observation). This is a practical style, a combination between the abstract-conceptual and the active-experimental types. This type of student is oriented toward finding the practical application of ideas and theories. They positively assess the opportunity to work actively on well-structured educational tasks and prefer learning on a trial and error basis in a safe environment at school. The efficient teacher for them is the one who is an instructor and from whom they receive practical directions and timely feedback. They define and solve problems, make decisions and work well alone. They also are characterized by deductive thinking. These types of students are good at formulating goals, planning their activities, and knowing how to find the information. They see the applicable aspects of the theory and their work is very well structured.”
The diagnosis of students’ learning styles is of prime importance for this research work. According to Griggs (Griggs, 1991, p. 3), there are “three instruments for assessing a learning style.” The Learning Style Inventory-Primary Version (Perrin, 1981) for children in kindergarten through grade two is a pictorial questionnaire.
Methods
The below presentation offers different ways to apply Kolb’s theory in the context of the education in mathematics in Grade 3 for solving mathematical text tasks.
The first stage of the learning process – the concrete experience – is based on the experience gathered by the students in Grade 1 and Grade 2 for solving ordinary text tasks whose solution requires only one arithmetic operation and composite text tasks in Grade 2 whose solution requires two arithmetic operations. 1. At this stage, the teacher, using the method of discussion update the knowledge, skills, and the acquired cognitive experience of the third graders regarding the text tasks described above.
During the second stage (the stage of reflexive observation) an intellectual and personal reflection and self-reflection is taking part in respect of the ways of solving different types of text tasks. This is aimed at revealing the meaning of the mathematical operations of addition, subtraction, multiplication, and division; at revealing different relations between numbers; at revealing the connections between the components and the results from the four arithmetic operations. This stage can be referred to as the first part of the process of solving a text task (understanding the content of the task) defined by D. Poya (Poya, 1972). Under the lead and the supervision of the teacher the third graders reverse back to their experience and perform analysis and synthesis to assess the suitability of the chosen way for solving the task. They also consider the possibility of more rational and easier ways to solve the task and if such are found, then how to apply them. The teacher is using the method of discussion and applies the methods of discussion and heuristic discussion through which he directs the students towards clarification of ways used to solve text tasks and to analyze the reasoning, and the performed activities.
During the third stage (abstract conceptualization) the students formulate a different hypothesis for solving the problem situations imposed by the text tasks. The teacher applies the productive method modeling and supports their work with auxiliary models. There are the following options for the creation of the models: they are composed after the analysis of the content of the text task done jointly by the teacher and the students. After that, the student fills in the numerical data in the model by themselves or with the assistance of the teacher using the method discussion (a reproductive discussion or a discussion with elements of heuristic).
During the fourth stage (the stage of active experimenting) the third graders work on the second step (analysis of the solution and composition of a plan for solving the task) and on the third step (execution of the plan for solving the task) of the process for solving a text task as defined by Poya (Poya, 1972). The students analyze the proposed way of solving the task (namely the mathematical numerical expressions), and they determine if any changes are needed or if there are any mistakes. They also discuss any other possible options for solving the task in question. The teacher applies the method of problem-productive exercise and exercise on analogy
In the methodology work problem-productive (indirect) strategies of education were applied. They are directed to the creation of pedagogy conditions for effective work in respect of generating ideas, applying solutions, research, proving, planning and assessment during the process of task solving by students. The main characteristic of this process is the transfer of already acquired the students’ knowledge and skills for solving tasks in new, creative situations or in a familiar situation to find new knowledge. Private-methodical/mathematical, developing, heuristic and person-oriented technologies of education are used.
The technology of education is oriented to a particular subject. It is also educational, informational, developing, and self-developing. The competency approach, the system-acting, the researching, the reflexive, the interactive, and the human-personal approaches are important components in its procedural side. The choice of the concrete method by the teacher depends on the concrete educational content related to solving text tasks, the stage of Kolb’s cycle, and the learning styles of the students. They perform activities on reproductive and productive-creative levels.
One of the composite text tasks which the Grade 3 students solve is given below:
The Ivanovs family saved 1345 lv. They bought a washing machine for 610 lv and a dishwasher for 476 lv. How much money they had left?
During the first stage (the stage of concrete experience) the experience gathered by the students so far relates to solving simple or composite text tasks aimed at clarifying the meaning of the operations addition and subtraction as well as at writing the solution of the task in two ways and namely with the use of two numerical expressions or with one numerical expression with brackets.
During the second stage (the stage of reflexive observation) the students reflect on ways to solve these types of tasks using their own experience.
During the third stage (the stage of abstract conceptualization) the teacher applies the method of problem-productive exercise through which the known and the unknown objects in the text tasks are getting identified. Students present their own hypotheses in reply to the imposed questions and make an abbreviated record of the task thus facilitating the transition from the external to the internal structure of the task.
If during their work in the fourth stage of Kolb’s cycle the third graders determine only one of the ways to solve the task, the teacher using a heuristic discussion with them shows the second way of solving the task as well. The problem-productive strategy of education applied by him helps the students to solve the problem situation embedded in the text task. The differences in the analytic-synthetic way of reasoning of both solutions are discussed.
Table 1. Solution of the task
|
First solution: |
Second solution |
|
610 + 476 = 1 086 |
1 345 – 610 = 735 |
|
1 345 – 1 086 = 259 or 1 345 – (610 + 476) = 259 |
735 – 476 = 259 or (1 345 – 610) – 476 = 259 |
|
Answer: Ivanov”s family remained with 259 lv left. |
|
Going through the four stages of Kolb’s model helps to improve students’ knowledge and skills to perform analytic-synthetic reasoning and to search for more than one solution to a given text task.
One of the types of text tasks according to the Rogier’s (Rogiers, 1985, pp. 229–234) classification is the so-called “open” task. For this type of task students independently search for all or for some numerical data and also allow different answers.
Below is an example of how the work on one of the “open” tasks from the methodology system shall be carried out, which was used in the study:
Stage 1 (CE): The work starts with updating the concrete experience of the students in respect of traveling (family trips or traveling with their classmates) in the country along different routes. They share details of their trips and namely which town their traveling started from, which towns they passed through and where their trip ended. They recall the algorithms of work used so far and the specifics of the activities related to data collection from different sources.
Stage 2 (RO): The teacher divides the students into teams of 3 and 4. They do reasoning on questions like If we pass through other towns in the country, what will change (parameters like length in kilometers of the route and the traveling time).
Stage 3 (AC): The teacher presents different routes from the Town of Stara Zagora to towns in East-West, North, and South Bulgaria. One reliable tool to assist the students is a map on the wall where all optional routes are schematically marked.
Stage 4 (AE): Each one of the teams receives the task to compose and describe the different routes from the Town of Stara Zagora to another town in the country (for example, the Town of Varna in East Bulgaria); collecting data for the distance of the route in kilometers and to write it down on a worksheet prepared by the teacher in advance. This is the first problem task that students must solve.
There are two options for the teacher to do his methodology work. The first option is to combine two organizational class-lesson forms of education – excursion, and lesson. The excursion is organized to a railway station or a bus station. The students shall be informed about the purpose of it in advance as well as about the tasks which they have to work on. From the timetable and other sources, they collect information about the duration of the trip by train or by bus between the towns in question and write it down in their worksheets. Using other sources of information designated by the teacher the students also collect data about the distances between the towns. This practical productive work helps the students to develop skills for collecting information from different sources. The second option is to use only one organizational form and namely a lesson in a class environment.
Stage 5 (CE): The students present the routes developed by them as well as the data they have collected for these routes – the distance in kilometers and the traveling time between the towns.
Stage 6 (RO): The third graders divided into groups to discuss different questions that arose during their presentations.
Stage 7 (AC): Considering the chosen routes the students formulate and present hypotheses about the different types of text tasks they may compose – text tasks to reveal the meaning of the mathematical operations addition and text tasks from different comparisons using the operations addition and subtraction.
Stage 8 (AE): The teams compose text tasks using the collected data and consequently solve them. They present these tasks to the class and discuss them. At this stage, students solve problem situations through composing text tasks.
“The students’ interest is provoked by the fact that they feel the need of diverse perception and actions leading to various emotional experiences while traveling and interacting with the surrounding world.” (Zheleva-Terzieva, 2019, pp. 21–28)
The productive methods used by the teacher in his methodology work are problem-seeking exercises, exercises of creative character, problem-seeking (heuristic) discussion, problem-seeking practical work, solving problem tasks by analogy, and heuristic (partial-research method), modeling, etc.
Through the above-described process solving of the “open” task, the students with accommodative learning styles can be included in new and unknown educational situations where to think over how to proceed. The teacher shall apply an indirect (problem-productive) strategy of education which is preferred by this type of student. The exact and logical presentation by the teacher during his joint work with the students corresponds to the preferences of the students with assimilative learning styles. The motivating presentation of the cognitive problems to them will facilitate their active participation in the process of problem-solving, otherwise, they will grudgingly participate in a random and aimless study of such problems. For students with divergent learning styles is important to study the situation in the “open” task from different points of view. They identify the problems in the task and produce new and creative solutions. The students with convergent learning styles define and solve problems during the process of working with the task. Assigning them to work on their own facilitates the use of the "strong" characteristics of their learning style. Students formulate the goal, plan their work and successfully find the necessary information related to the traveling routes.
The experimental work was carried out with students from Grade 3 of the Second Elementary school Petko Rachov Slaveykov in the Town of Stara Zagora for the period 2015 to 2021. To identify the learning style of the Grade 3 students subjected to the research, the “Kolb’s Styles” Questionnaire was used. This is a methodology for researching the way students prefer to study the educational material. The Questionnaire contains 9 questions every one of which has got 4 answers to choose from.
Results
For the purposes of the experimental work, two tests have been used. One of the tests was for the entry diagnostic of the students and was applied at the beginning of the school year. The second test was for the exit diagnostic of the students and was done after applying the new methodology system of work. The researcher studied some of the qualities of the two tests such as their difficulty and separating force of the tasks in the tests. Each one of the tests consists of eight tasks. The first task is of ordinary nature while the second and the third tasks are composed of text tasks that need their solving up to 3 calculations with direct use of relations. The fourth task is also a standard task. The fifth and the sixth tasks are again composed tasks however with indirect use of relations. The seventh task requires students to compose a text task by given numerical data. The eighth task requires the same but students must compose the text task using a schematic auxiliary model (drawing).
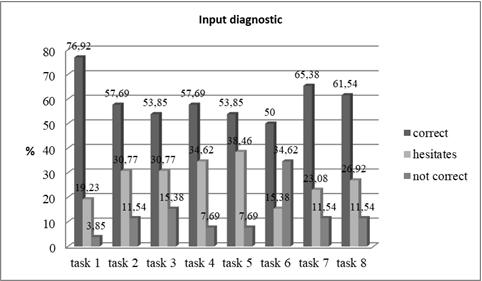
The results from the entry diagnostic are presented in Figure 2.
Figure 2. Entry diagnostic of Grade 3 students’ knowledge and skills to solve text tasks
They demonstrate that the third graders have acquired the knowledge and the skills needed to solve both standard text tasks using only one calculation and composed text tasks that need up to two calculations for their solving with direct use of the relations “with … more than …”, “with … less than …”, “… times more than …” and “… times less than …”. The entry diagnostic test helped to find out that …% of the students can compose text tasks by a picture with numerical data, numerical expression, and table.
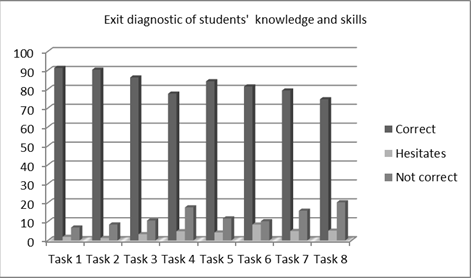
The exit diagnostic is done in 2021 and the results are presented and analyzed graphically in the below diagram (Figure 3).
Figure 3. Exit diagnostic of Grade 3 students’ knowledge and skills to solve text tasks
As a result of the experimental work, it was found out that after the exit diagnostic 91, 23% of the third graders using numerical expressions correctly model situations described by the direct use of the relation “with …. more than ….”. 8, 42% of the students make mistakes when model situations described by the direct use of the relation “with … less than ….”. 86,16% of the students correctly solve text tasks with indirect use of the relation “with …. more than …”. 17,52% of the students make mistakes when solving text tasks with indirect use of the relation “with … less than ….”. Using numerical expressions 84,16% of the students correctly model situations described by direct use of the relation “… times more than …”. 10,18% of the students make mistakes when using numerical expressions for modeling situations described by direct use of the relation “… times less than …”. 79,28% of the third graders correctly solve text tasks with indirect use of the relation “… times more than …”. 20,16% of the children make mistakes when solving text tasks with indirect use of the relation “… times less than …”. The difference in the results was proved to be statistically significant.
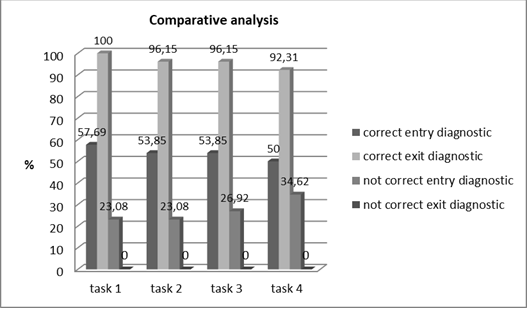
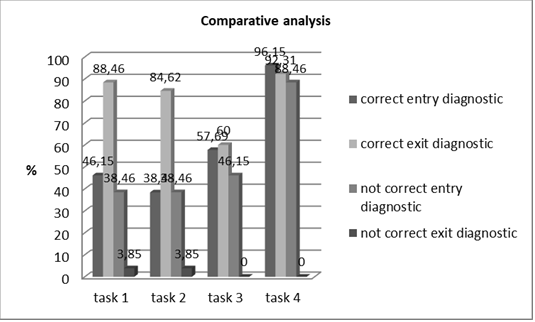
The following two diagrams graphically present the data from the comparative analysis between the entry and the exit diagnostic of the knowledge and the skills of the third graders to solve text tasks.
Figure 4. Comparative analysis between the entry and the exit diagnostic of the knowledge and the skills of the third graders to solve text tasks
The data in Figure 4. show that between the respective shares of the students subjected to the study there is a statistically significant difference seen in the results from the entry and the exit diagnostic in respect of their skills to solve standard text tasks with direct and indirect use of the relations “with … more than …”, “with … less than …”, “… times more than …” and “… times less than …”. (First criteria, 1., 2., 3., and 4. Indicators)
Below are presented the calculations and the comparison of the respective shares of parameters studied during the work with the experimental class at the beginning and at the end of the study.
For Task 1:
U calc. = 6, 188 for α = 0,05 probability for mistake U (α) table = 2,06
For Task 2:
U calc. = 4, 0026 for α = 0,05 probability for mistake U (α) table = 2,06
For Task 3:
U calc. = 4, 105 for α = 0,05 probability for mistake U (α) table = 2,06
For Task 4:
U calc. = 4, 038 for α = 0,05 probability for mistake U (α) table = 2,06
The data in Figure 5. show that between the respective shares of the students subjected to the study there is a statistically significant difference seen in the results from the entry and the exit diagnostic in respect of their skills to solve composed text tasks requiring up to 3 calculations with direct and indirect use of the relations “with … more than …”, “with … less than …”, “… times more than …” and “… times less than …”. (Second criteria, 1., 2., 3., 4. and 5. Indicators)
Figure 5. Comparative analysis between the entry and the exit diagnostic of the knowledge and the skills of the third graders to solve text tasks
For Task 5:
U calc. = 3, 889 for α = 0,05 probability for mistake U (α) table = 2,06
For Task 6:
U calc. = 3, 647 for α = 0,05 probability for mistake U (α) table = 2,06
For Task 6:
U calc. = 3, 801 for α = 0,05 probability for mistake U (α) table = 2,06
For Task 7:
U calc. = 4, 367 fpr α = 0,05 probability for mistake U (α) table = 2,06
For Task 8:
U calc. = 3, 647 for α = 0,05 probability for mistake U (α) table = 2,06
For Task 9:
U calc. = 4, 105 for α = 0,05 probability for mistake U (α) table = 2,06
The reasoning demonstrated by the Grade 3 students on the performed activities during the task-solving process showed the improvement of their reflexive skills. These skills are getting piled up and developed during the process of education in mathematics and represent a complex system of knowledge, skills, relations, self-control, self-development, self-assessment, etc. Students upgrade the skills in question with every next stage of their education. Teachers must be familiar with the steps of the Korthagen model related to the process of development of reflexive skills and namely action, looking back to the action, understanding the main aspects, creation of alternative methods of action, and testing which is a new action itself and consequently, a starting point of a new cycle.
The empiric study presents an observation and the results of it are introduced in two observation protocols – the first protocol relates to the entry diagnostic and the second one – to the exit diagnostic. The information in the protocols reflects the correctness of the student’s reasoning and explanations regarding the activities performed by them during the four stages of the text task solving process – reasoning on the text task content, making a plan for its solving, execution of the plan and looking back to the whole process completed so far. The main reasoning is getting performed exactly at this last stage. The results received from the test show that the correct reasoning increased from 20% to 34%.
Conclusions
Based on the results of the research work the following conclusions can be made:
After completing the longitudinal research, it was found that Kolb’s model of experimental learning can be successfully applied not only in University education but also in the education in mathematics for Grade 3 of Primary school.
After applying the developed methodology system of work the following was achieved:
- systematic transition through Kolb’s four stages (concrete experience, reflexive observation, abstract conceptualization, and active experimenting) during solving text tasks in Grade 3.
- facilitates the overcoming of re-productivity in the practical activities of the students. As a result of this, education in mathematics is not only reproductive but also flexible learning.
- facilitates the development in the students of a higher level of knowledge, skills, and competencies from competency Cluster Modelling, related to extracting information from different sources like tables and drawings, modeling of situations from the real world using mathematical numerical expressions as well as summarizing the results received after solving a particular problem.
The following is getting completely developed:
- Students’ knowledge and skills to solve ordinary and composed text tasks with direct and indirect use of relations;
- Students’ knowledge and skills to compose text tasks by given pictures with numerical data, tables, and numerical expressions;
- Grade 3 students’ reflexive skills for solving different types of text tasks.
The use of Kolb’s model of experimental learning helps to increase students’ activity during the educational process in mathematics, form them reflexive skills, and make them learn by consideration of their experience.
References
Corno, L., & Snow, R. E. (1985). Adapting teaching to individual differences among learners. In M.C. Wittrock, ed., Handbook of research on Teaching, 3rd ed., New York, N.Y.: Macmillan and Co., 605–620.
Doncheva, J. (2017). Principles of training in line with the new thinking and action. SEA - Conf., 3 International Conference (p. 74). Naval Academy, Constanta.
Dunn, R., & Dunn K., Price, G. (1982). Manual: Productivity environmental preference survey. Lawrence, KS: Price Systems.
Dunn, R., & Dunn K., Price, G. (1985). Manual: Learning style inventory. Lawrence, KS: Price Systems.
Felder, R. (1996). Maters of styles, ASEE Prism, 6 (December 1996), № 4, pp. 18–23. Retrieved from http://www.ncsu.edu/felder-public/Papers/LS-Prism.htm.
Fielding, M. (1994). Valuing difference in teachers and learners: Building on Kolb’s learning styles to develop a language of teaching and learning. The Curriculum Journal 5, 395.
Gibbs, G. (1988). Learning by Doing: A Guide to Teaching and Learning Methods. London, UK: Further Education Unit, 20.
Griggs, Sh. (1991). Learning styles counseling. ERIC: Digest, ERIC Clearinghouse on Counseling and Personnel Services Ann Arbor MI., ERIC Identifier: ED341890, 2.
Healey, M., & Jenkins A. (2000). Kolb's Experiential Learning Theory and Its Application in Geography in Higher Education, Journal of Geography, 99, 185–195.
Ivanov, I. (2004). Stilove na poznanie i uchene. Teorii. Diagnostika. Etnicheski I polovi variaciii v Bulgaria [Styles of knowledge and learning. Theories. Diagnostic. Ethnical and sex variations in Bulgaria]. Shoumen, 30.
Jenkins, A. (1998). Curriculum Design in Geography. Cheltenham, UK: Geography Discipline Network, Cheltenham and Gloucester College of Higher Education.
Keefe, J. W. (1979). Learning style: An overview. In NASSP's Student learning styles: Diagnosing and prescribing programs. (pp. 1–17). Reston, VA: National Association of Secondary School Principals.
Kolb, D. A. (1984). Experiential Learning: Experience as the Source of Learning and Development. Englewood Cliffs, New Jersey: Prentice-Hall, 38.
Krumova, Al. (2018). Kognitiven stil i stilove na uchene pri uchenicite [Cognitive style and learning styles of students]. Pre-school and school education, No 1.
Lecheva, G. (2009). Stilovete na uchene kato pedagogicheska kompetentnost za raznoobrazyavane na prepodavatelskite strategii [Learning styles as a pedagogy competency for diversification of teaching strategies]. Scientific works of the University of Russe, Volume 48, series 6.2.
Mihova, М. (2002). Prepodavaneto i ucheneto. Teorii. Stilove. Modeli [Teaching and studying. Theories. Styles. Models]. Veliko Tarnovo, 79.
Perrin, J. (1981). Primary version: Learning style inventory. Jamaica, NY: Learning Style Network, St. John's University.
Poya, D. (1972). Kak da se reshava zadacha [How to solve mathematical tasks]. National education.
Riding, R. (1997). On the nature of cognitive styles. Educational psychology, 17, 29–49.
Riding, R., & Chema I. (1991). Cognitive styles: an overview and integration. Educational psychology, 11(3&4), 193–215.
Rogiers, H. (1985). Guide mathematique de base pour l’ecole primaire – geometrie, grandeurs, problems. Bruxelles, 229-234.
Zheleva-Terzieva, D. (2019). Educational Dimensions of Sports and Animation Activity in Educational Environment. Pedagogical Review - Scientific Journal of Educational Issues, Ss. Cyril and Methodius” in Skopje, Faculty of Pedagogy “St. Kliment Ohridski”- Skopje, year 10, issues 2, 21–28.
Zhelyazkova, Zl. (2018). Efektivno uchene na angliyska gramatika [Effective learning of English grammar]. St. Zagora, Trakia University, ISBN: 978-954-314-085-5, 104.