Igrifikacija u primarnom obrazovanju
Ivana Medica Ružić1, Mario Dumančić21 Osnovna škola Jože Šurana, Višnjan 2 Sveučilište u Zagrebu, Učiteljski fakultet |
|
Digitalne obrazovne tehnologije |
Broj rada: 34 |
Izvorni znanstveni rad |
Sažetak |
|
Ako pitate učenike “Što je to rad?” odgovorit će vam “škola i domaća zadaća”. Ali ako ih pitate “Što je to igra?” odgovorit će vam videoigre, igrice na računalu, mobitelu, tabletu. Jasno je da bi trebao postojati način da učenicima pomognemo da uče iz onog u čemu su najbolji, a to je IGRANJE. Ovo je jedan od razloga zbog čega je igrifikacija veoma značajna u odgoju i obrazovanju. U ovom ćemo radu prikazati povijest korištenja igra i njihovu važnost, kao i važnost igrifikacije u odgoju i obrazovanju. Također u radu ćemo prikazati rezultate kvazi eksperimentalnog istraživanja u kojem je bio cilj utvrditi mogućnost primjene igrifikacije u nastavi matematike, te ispitati utjecaj igrifikacije na ishod učenja u nastavnom predmetu Matematika u osnovnoj školi. |
|
Ključne riječi |
|
igra; igrifikacija; kvazi eksperimentalno istraživanje; odgoj; primarno obrazovanje; učenici |
Povijest igre
Povijest igara i njihova uporaba u obrazovanju započela je davno. Igra je vrlo važna komponenta razvoja svakog pojedinca i društva. Postoje različiti dokazi o korištenju igre u obrazovanju u povijesti ljudskog društva no, među prvim pisanim dokazima korištenja igre u obrazovanju pronalazimo kod Platona. Platon je u svojim djelima opravdao uporabu igara u obrazovanju, te ju je smatrao kao glavnu obrazovnu metode za djecu. Nakon njega Aristotel, Platonov učenik, također je prihvatio važnost igara za obrazovanje, u svojim je djelima Politika i Nikomahova etika, zagovarao potrebu za igrama u dječjoj dobi. J.A.Comenius (1592.-1670.), veliki europski pedagog i teolog, smatrao je igru vrlo važnim elementom odgoja, kao što bi i samo obrazovanje trebalo biti razigrano i radosno. Comenius je također naglasio da djeca moraju igrati i grupne igre kako bi razvili svoje društvene vještine. Prema njegovom mišljenju, igre blagotvorno djeluju na zdravlje djece i oni razvijaju svoja osjetila, pamćenje, prosudbu, radni zanos i rječitost.
Francuski prosvjetitelj J. J. Rousseau (1712.–1778.) u svojem djelu Emil ili O odgoju brani humanistička mišljenja o djetinjstvu. Prema Rousseau, igra je prirodna aktivnost djeteta koja najbolje zadovoljava njegovu potrebu za aktivnošću. Njemački pedagog J. H. Pestalozzi (1746.-1827.) dalje je razvio Rousseauove ideje. Pestalozzi je naglašavao važnost učenje kroz aktivnost kako bi pokušao potaknuti učenika da pokaže svoje interese, a jedna takva aktivnost je bila igra. F.W.A.Frobel (1782–1852) je također vjerovao u veliku važnost igara u obrazovanju i odgoju te smatra kako su igre sredstvo zdrave evolucije mladih ljudi i da su igranje i igre najviši stupanj dječjeg razvoja.
Poznati psiholozi, filozofi i pedagozi izradili su detaljne analize igara i njihovu važnost u životu ljudi u 19. stoljeću. Jedan od njih je i njemački dramski pisac, J. W. Goethe (1749.1832.) koji je istaknuo važnost igara u obrazovanju, a posebno su ga zanimali maštoviti i dramatični elementi igara. Smatrao je da igre razvijaju maštu, pamćenje i emocionalnost, a igru je shvaćao kao sredstvo općeg osobnog razvoja.
Prema njemačkom pjesniku i filozofu, F. Schilleru (1759.–1805.), igra pruža pojedincima da se slobodno izraze i tako postignu ljepši život. H. Spencer (1820.–1903.), engleski filozof, sociolog i edukator, zagovarao je obrazovanje i odgoj koje je usmjereno na pripremu za život. Po njegovom mišljenju, igre su izraz potrebe za otpuštanjem viška energije. Njemački psiholog i edukator K. Groos (1861.–1946.) je razradio prvi sveobuhvatni koncept razloga i značenja razigranog ponašanja. Smatra igre kao oblik instinktivnog ponašanja koje gradi temelje za razvoj inteligencije. Groosovo mišljenje da su igre sredstvo općeg razvoja je široko prihvaćeno.
Nadalje, važna talijanska edukatorica, M. Montessori (1870.–1952.), je razradila program podrške za pomoć učenicima s poremećajem pisanja i čitanja te osmislila sustav odgoja i obrazovanja za djecu. Da bi razvila sposobnost i vještine, Montessori često koristi igre kao prirodni oblik aktivnosti za djecu. J. Piaget (1896.–1980.) i B. Inhelder (1913.–1997.), renomirani francuski psiholozi, proveli su sveobuhvatno proučavanje uloge igara u dječjim životima. Prema istraživanjima Piageta i Inheldera, igre razvijaju senzorno-motoričke sposobnosti, emocionalna i intelektualna područja, kao i maštu. Ruski psiholog L. S. Vygotsky (1896.–1934.), detaljno je proučavao kognitivni razvoj djece. On je uglavnom proučavao odnos jezika i mišljenja te naglašavao ulogu socijalizacije igara. Američki psiholog J. S. Bruner (1915.) se bavio djelotvornim načinom obrazovanja i odgovarajućim uređenjem kurikuluma na temelju teorija konstruktivizma. Bruner je naglasio sposobnost djece da se usredotoče na aktivnost tijekom igre, na način razigranog ponašanja i daljnje dobivanje informacija. Stoga Bruner smatra da će igre biti odgovarajuća obrazovna metoda. Utemeljitelj pragmatizma J. Dewey (1859.–1952.), naglašava prirodnu kognitivnu i odgojnu funkciju igre te pridaje veliku važnost obrazovnoj ulozi igara.
Steiner (1861.–1925.), austrijski znanstvenik i filozof, razradio je metodu odgoja koja se koristi u Waldorfskoj školi. On smatra da obrazovanje treba uzeti u obzir trenutne potrebe djece koje se mijenjaju sa njihovim fizičkim, mentalnim i emocionalnim razvojem te zahtijeva da su glavne aktivnosti djece ispod 7 godina, igre.
GFEN - Francuska skupina novog obrazovanja - GFEN (Groupe Fran¸cais d‘´education nouvelle) ima značajnu obrazovnu ulogu u igrama. Njihov didaktički pristup je temeljen na važnosti igara, tj. na otkrivanju da svaka igra, uz poticanje aktivnosti i užitka, ima mnoge specifičnosti u svojoj prirodi.
Važnost igre
Kao što smo vidjeli, važnost igre za obrazovanje je ideja koja se razvija još od antičkih vremena, što potvrđuju i mišljenja brojnih renomiranih i uglednih znanstvenika. U današnjim vremenima igra je aktivnost koja je atraktivna za većinu učenika, ali i za većinu odraslog stanovništva. Trenutno igrifikacija postaje sve popularnija.
Naziv (Gamification- prvi upotrijebio Nick Pelling 2003. Kompanijama da unaprijede proizvode kroz platforme za zabavu)
Definicija (Igrifikacija je proces koji koristi igračko razmišljanje i mehaniku igre s ciljem motiviranja ljudi/učenika i rješavanja problema. (Zichermann, 2010). Prema Karl M. Kappu (2012) igrifikacija je proces korištenja osnova mehanike svake igre, estetike i igračkog razmišljanja u cilju angažiranja, motiviranja ljudi na način da se promiče učenje na bolje i riješi zadani problem.)
Uporaba (Marketing-nagrađivanje klijenata, zabava; Upravljanje ljudskim resursima- nagrađivanje zaposlenika, razvoj kreativnosti i suradnje; Inovativni turistički proizvodi – Team-building, LARP (Live Action Role Play); Vojne svrhe - američki vojnici su trenirani na koji način generirati ideje.; HIV- u medicini je u 2. tjedna razotkrivena struktura koja pomaže u daljnjem napretku izlječenja HIV pozitivnih osoba (15 godina tražili))
Igrifikacija u nastavi-obrazovni pristup u kojem bi se učenike motiviralo na učenje korištenjem dizajna i elemenata video igra i igra
Zašto? Vrijeme koje učenici provedu na nastavi u školi od petog razreda pa sve do završetka nastave u srednjoj školi, jednako je vremenu od 10 000 sati. Jednako toliko svaka prosječna osoba provede igrajući online igre do svoji 21. godine života (McGonigal, 2010). Konvencionalne metode postaju sve manje zanimljive, posebice novim generacijama (Dichev, 2014). Stoga začuđuje sama činjenica da se današnje generacije poučava samo na konvencionalan način, ako je dokazano da je suvremeni čovjek, tijekom odrastanja prosječno proveo dvanaest godina igrajući kompjuterske igre i videoigre. Način poučavanja treba se približiti takvom čovjeku i pomoći mu u učenju i razvijanju njegovih potencijala, a ne da mu bude prepreka i novina koja ga u tome zaustavlja.
Igrifikacija nastave
Svaki oblik nastave moguće je igrificirati, a to je moguće u slijedećih nekoliko koraka:
- Korak – DEFINIRANJE POLAZNIKA I NASTAVNIH UVIJETA – trajanje nastave, oblici rada, mjesto, vrijeme, te određivanje otežavajućih čimbenika
- Korak – DEFINIRANJE ISHODA UČENJA
- Korak – STRUKTURIRANJE AKTIVNOSTI- podjela nastavne cjeline ili obrazovnog programa na više faza ili stupnjeva (doprinosi lakšem ostvarivanju ciljeva i svladavanju prepreka)
- Korak – ODREĐIVANJE PRIMJENJIVIH ELEMENATA IGRIFIKACIJE U KONKRETNOJ NASTAVNOJ CJELINI: (Alati i jedinice za praćenje napretka učenika; Razina napretka; Jasna pravila, definirane obaveze i načini ispunjavanja; Povratna informacija)
- Korak – PRIMJENA ELEMENATA NASTAVE U CJELINI
Kako bi se igrifikacija u potpunosti integrirala i imala učinka ona mora sadržavati slijedeće TEMELJNE ELEMENTE U NASTAVI:
I.DRUŠTVENA POVEZANOST – dijeljenje zadataka, razmjena ideja, izražavanje mišljenja
II.ALATI ZA PRAĆENJE NAPRETKA – samo motivirajući (bodovi, značke, razine)
Vremensko ograničenje (učenik se natječe sa samim sobom)
III.POBOLJŠAVANJE UČENJA – element neophodan kako bi se sama igrifikacija mogla realizirati
IV.RAZMIŠLJANJE „GAMERA”, ODNOSNO IGRAČA – obuhvaćanje vještina vođenja stečene kroz rješavanje zadataka i prelaženje razina
V.RJEŠAVANJE PROBLEMA – u srži svake igre je da ohrabri ljude/učenike da se potrude kako bi dosegli svoj cilj (npr. pobijedili)
3 KLJUČNA NAČINA KAKO IGRIFICIRATI NASTAVU
- JEZIK – korištenje vokabulara karakterističnog za videoigre (pisanje ispita- poraziti čudovište; izrada prototipa-ispuniti misiju)
- OCJENJIVANJE – prilagoditi ocjenjivanje
Ne koristiti klasične ocjene već bodove koji se skupljaju dokazivanjem (npr. xy =ocjena ; 2500 xy =3; 3000 xy= 4; 3500 xy= 5)
- STRUKTURA NASTAVE – inkorporirati elemente igrifikacije
Uloga učenika- izabrati avatara, kodno ime
Uloga učitelja – dizajnirati nastavnu jedinicu koristeći elemente igrifikacije
Naime, igrifikacija je moderni obrazovni izazov koji uključuje poslove angažiranja učenika, poticanje novih interesa i pri tome zadržavanje njihove pozornosti i održavanje pozitivnog stava u okruženju u kojem se nalazi.
Da bismo ostvarili spomenute ciljeve važan je napor kako bismo održali bogato komunikacijsko okruženje koje potiče povratne informacije, ne samo između učitelja i učenika, nego i između samih učenika.
Ovi socijalno interaktivni mehanizmi, uz odgovarajuću razinu kontrole za poticanje i disciplinu, mogu biti dizajnirani na učinkovite načine za stvaranje “zabavnih” situacija učenja.
Kako bi dokazali učinkovitost igrifikacije (koja je igranje, ono što djeca vole i pri tome uče, moderan obrazovni trend u skladu sa razvitkom informacijsko-komunikacijskim tehnologijama) bilo bi korisno provjeriti na predmetu kao što je Matematika, gdje je dokazano da učenici postižu lošije rezultate (Baranović, 2006).
Matematika je jedan od predmeta u kojem postoji samo jedan točan rezultat na postavljeni problemski zadatak. Ona iziskuje veliku usredotočenost kako na sadržaj, tako i na logičko razmišljanje, kontinuitet u radu i automatizam.
Međutim nije rijetkost da mnoge predrasude zakoče učenikove sposobnosti posebno kada se radi o učenicima osnovnih škola i na taj način dovode do toga da učenikove sposobnosti uopće ne dođu do izražaja.
Tome pridonosi i godinama poznata tvrdnja kako je matematika teška, te kako gotovo svaki učenik ima problema s matematikom.
Sami roditelji veoma često izjavljuju rečenice poput: "Matematika mi nikad nije išla", "Ako sam s nekim predmetom u školi imao problema bila je to matematika", "Profesori iz matematike su uvijek strogi", "Poput djevojčica, i dječaci kao predmet koje najmanje vole najčešće navode kemiju, a zatim u istom postotku matematiku i hrvatski jezik." (Baranović, str. 247, 2006). Navedeni su razlozi zapravo ključni zašto će se u ovom radu odabrati predmet matematika.
Istraživanje
Cilj: Utvrditi mogućnost primjene igrifikacije u nastavi matematike, te ispitati utjecaj igrifikacije na ishode učenja u nastavnom predmetu Matematika u osnovnoj školi.
- Problem: Provjeriti razlikuju li se kontrolna i eksperimentalna skupina u usvojenosti nastavnog sadržaja iz matematike.
- Problem: Provjeriti razlikuju li se kontrolna i eksperimentalna skupina u razumijevanju nastavnog sadržaja iz matematike.
- Problem: Provjeriti razlikuju li se kontrolna i eksperimentalna skupina u primjeni nastavnog sadržaja iz matematike.
Na osnovu postavljenog cilja istraživanja kreirali smo slijedeće hipoteze:
H1: Kvazieksperimentalna i kvazikontrolna skupina ne razlikuju se u usvajanju nastavnog sadržaja iz matematike
H2: Kvazieksperimentalna i kvazikontrolna skupina ne razlikuju se u razumijevanju nastavnog sadržaja iz matematike
H3: Kvazieksperimentalna i kvazikontrolna skupina ne razlikuju se u primjeni znanja nastavnog sadržaja iz matematike
U glavnom istraživanju sudjelovalo je 168 učenika od 1. do 4. razreda jedne osnovne škole. Sudjelovao je približno isti broj učenika iz svakog razreda (nraz1=41, nraz2=43, nraz3=44, nraz4=40) te su učenici izjednačen s obzirom na spol nž=84, nm=84). Iz svakog razreda sudjelovala su po dva razredna odjela pri čemu su učenici jednog odjela sudjelovali u kvazieksperimantalnoj, dok su učenici drugog razrednog odjela sudjelovali u kvazikontrolnoj skupini.
Tablica 1. KOntrolna i kvazieksperimentalna grupa
|
|
Kontrolna (n=84) |
Eksperimentalna (n=84) |
|
Spol |
||
|
Muški |
50% |
50% |
|
Ženski |
50% |
50% |
|
Razred |
||
|
1. r |
23,8% |
25,0% |
|
2. r |
26,2% |
25,0% |
|
3. r |
26,2% |
26,2% |
|
4. r |
23,8% |
23,8% |
U glavnom istraživanju korišten je kvazieksperimentalni nacrt s jednom kvazieksperimentalnom i jednom kvazikontrolnom skupinom. Učenici kvaziksperimentalne skupine podučavani su uz primjenu igrifikacije u nastavi matematike, dok su učenici kvazikontrolne skupine podučavani konvencionalnim nastavnim metodama. U obje skupine obuhvaćen je isti nastavni sadržaj.
U istraživanju je korištena je jedna nezavisna i tri zavisne varijable.
Nezavisnu varijablu predstavlja različit oblik nastavnog sadržaja (igrifikacija/klasična nastava) kojem su ispitanici bili izloženi ovisno o tome kojoj su skupini pripadali.
Prva zavisna varijabla je količina informacija iz obrađene tematske cjeline koju su učenici upamtili. Ova varijabla je kvantitativna i operacionalizirana je rezultatom u testu znanja objektivnog tipa.
Druga zavisna varijabla jest razumijevanje nastavnog sadržaja, ona je kvantitativna i operacionalizirana kao rezultat na testu znanja objektivnog tipa.
Treća zavisna varijabla u ovom istraživanju je primjena nastavnog sadržaja, ona je također kvantitativna i operacionalizirana je kao rezultat na testu znanja objektivnog tipa.
Instrumenti
Za potrebu mjerenja znanja iz matematike kod učenika 1. do 4. razreda u pilot-istraživanju konstruirani su testovi znanja objektivnog tipa. Za svaki razred konstruirana su po dva testa znanja kako bi se ispitao nastavni sadržaj iz dvije različite nastavne jedinice unutar jednog razreda.
Ukupno je za potrebu ovog istraživanja konstruirano 8 testova znanja ciljem mjerenja tri ishoda u 8 nastavnih cjelina.
U svim je testovima označavanje točnog odgovora u zadatku bilo u obliku zaokruživanja jednog od ponuđenih odgovora ili u obliku upisivanja kratkog odgovora na za to predviđeno mjesto jednom ili nekoliko riječi.
Osim ukupnog rezultata u testu, za svakog ispitanika moguće je formirati i tri dodatna rezultata, koji predstavljaju tri ishoda učenja nastavnog sadržaja iz matematike, a to su: 1) usvajanje sadržaja; 2) razumijevanje sadržaja; 3) primjena znanja.
Tablica 2. Pregled korištenih instrumenata
|
Razred |
Test znanja |
Obuhvaćena nastavna cjelina iz Matematike |
ukupan br. zadataka |
Cronbach α |
|
1. raz. |
1 |
C1 - Pribrojnici i zbroj; Zamjena mjesta pribrojnika |
19 |
0,54 |
|
2 |
C2 - Umanjenik, umanjitelj, razlika - obrada |
20 |
0,81 |
|
|
2. raz. |
3 |
C1 - Množenje broja 2, 5, 10, 1 i 0; Dijeljenje brojevima 2, 5, i 10 |
20 |
0,86 |
|
4 |
C2 - Množenje i dijeljenje do 100 |
21 |
0,82 |
|
|
3. raz. |
5 |
C1 - Pisano množenje (43·2, 26·3, 32·4, 43·5) |
20 |
0,77 |
|
6 |
C2 - Ravnina, likovi u ravnini; Pravac, polupravac i dužina kao dijelovi pravca; Mjerenje dužine |
20 |
0,62 |
|
|
4. raz. |
7 |
C1 - Površina pravokutnika i kvadrata |
20 |
0,74 |
|
8 |
C2 - Kocka i kvadar; Obujam kocke |
17 |
0,51 |
Prilikom konstrukcije testova vodilo se računa o tome da svaka nastavna cjelina bude obuhvaćena podjednakim brojem zadataka pa prema tome test sadrži između 17 i 21 zadataka.
Tablica 3: Udio zadataka (%) koji mjere pojedine ishode u ukupnom broju zadataka u testu prikazan s obzirom na razred, nastavnu cjelinu i vrstu ishoda
|
Prvi razred |
|
Drugi razred |
|
Treći razred |
|
Četvrti razred |
|
|
C1 |
C2 |
|
C1 |
C2 |
|
C1 |
C2 |
|
C1 |
C2 |
|
|||||||
|
Usvajanje |
42 |
15 |
50 |
38 |
15 |
50 |
35 |
47 |
|
||||||||||
|
Razumijevanje |
37 |
75 |
30 |
29 |
40 |
40 |
30 |
24 |
|
||||||||||
|
Primjena |
21 |
10 |
20 |
33 |
45 |
10 |
35 |
29 |
|
||||||||||
|
Ukupno |
100 |
100 |
|
100 |
100 |
|
100 |
100 |
|
100 |
100 |
|
|||||||
Svi testovi primjereno su saturirani zadacima koji mjere različite ishode (10% do 75%). Iznimka je jedino test za prvi razred koji se odnosi na nastavnu cjelinu C2 koji je nešto više saturiran zadacima razumijevanja (75%) u odnosu na zadatke usvajanja (15%) i primjene (10%).
No može se zaključiti da je u svih osam testova ostvarena primjerena raspodjela udjela pojedine vrste zadataka u ukupnom broju zadataka u testovima znanja, što osigurava adekvatno mjerenje sva tri očekivana ishoda: usvajanje, razumijevanje i primjena nastavnog sadržaja.
Postupak istraživanja
U kvazieksperimentalnoj i kvazikontrolnoj skupni obrađivale su se po dvije nastavne jedinice iz područja matematike. Svaka nastavna jedinica činila je zasebnu tematsku cjelinu, a obrađivale su se na način da j obrada ili ponavljanje s učenicima odrađeno samo na prvom školskom satu, dok je drugi školski sat poslužio kao distraktor nakon kojeg je uslijedilo rješavanje nizova zadataka objektivnog tipa. Trajanje obrade nastavne jedinice je tri mjeseca ili do dovršetka istraživanja. U kvazieksperimentalnoj skupini obrađivala se tematska cjelina uz pomoć upotrebe igrifikacije u nastavi, dok se u kontrolnoj skupini tematska cjelina obrađivala konvencionalnim metodama učitelja provoditelja istraživanja.
Istraživanje se provodilo pomoću programa Zondle i Arcademics Plus u kvazieksperimentalnoj skupini, dok se u kontrolnoj skupini odvijalo kao i do sada. Provoditelj/učitelj u kvazieksperimentalnoj i kontrolnoj skupini bio je isti kako način učenja i poučavanja uz upotrebu igrifikacije i bez njene upotrebe ne bi utjecao na rezultate istraživanja. Programi Zondle i Arcademics Plus omogućuju učenicima i učiteljima sudjelovanje u nastavi u kojoj je zastupljena upotreba igrifikacije. Spomenuti su programi samo dio nastave u kojoj je zastupljena upotreba igrifikacije te uvelike pomaže i učeniku i učitelju u radu na usvajanju i razumijevanju nastavnog sadržaja.
Statistička analiza
U radu su prikazani deskriptivni podaci korištenih varijabli. Razlike između kvazikontrolne i kvazieksperimentalne skupine provjerene su t testom pri čemu je statistička značajnost testirana uz rizik manji od 5%. Sve analize provedene su u statističkom paketu SPSS v23.
Rezultati i rasprava
Prikupljeni su odgovori učenika od prvog do četvrtog razreda osnovne škole na testovima znanja ovisno o razredu koji učenik trenutačno pohađa. Podaci su analizirani zasebno za prvi, drugi, treći i četvrti razred te su provedene odgovarajuće statističke analize. Svaki test je konstruiran na način da ne mjeri samo ukupno znanje već i usvojenost, razumijevanje i primjenu nastavnog sadržaja, a razlike u navedenim ishodima bit će ispitane kroz četiri postavljene hipoteze koje odgovaraju istraživačkim problemima istraživanja koje će biti prikazane kroz cjeline u rezultatima.
H1: Kvazieksperimentalna i kvazikontrolna skupina ne razlikuju se u usvajanju nastavnog sadržaja iz matematike
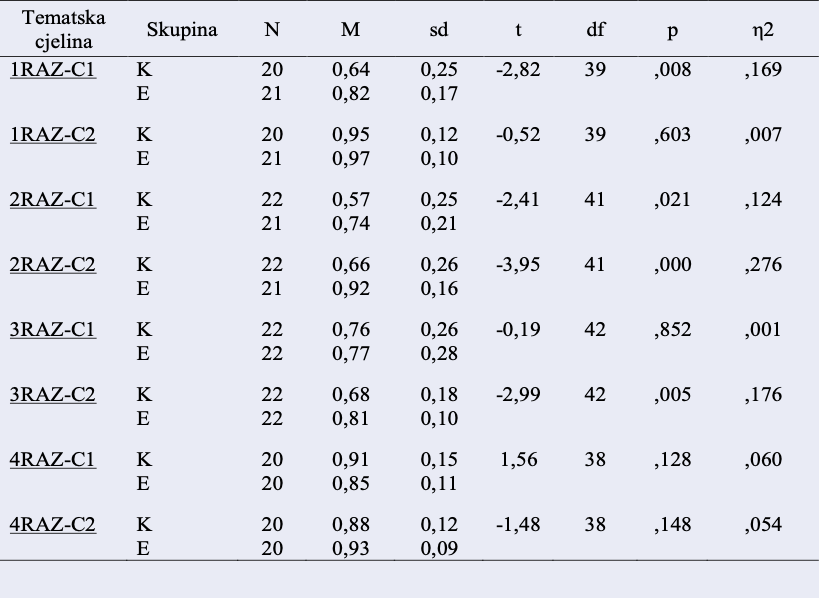
Značajne razlike u usvajanju nastavnog sadržaja između kontrolne i eksperimentalne skupine dobivene su u usvajanju nastavnog sadržaja prve cjeline kod učenika prvog razreda t(39) = −2.82, p < .05, η2=0.411), zatim u usvajanju nastavnog sadržaja prve cjeline kod učenika drugog razreda (t(41) = −2.41, p < .05, η2=0.352) te također u usvajanju nastavnog sadržaja druge cjeline kod učenika drugog razreda (t(41) = −3.95, p < .05, η2=0.525). Osim toga, statistički značajna razlika između kontrolne i eksperimentalne skupine dobivena je u usvajanju sadržaja druge cjeline kod učenika trećeg razreda (t(42) = −2.95, p < .05, η2=0.419). Sve navedene statistički značajne razlike dobivene su u smjeru postizanja boljeg uspjeha kod učenika eksperimentalne skupine (tablica 14).
Slično kao i kod postizanja ukupnog rezultata u testu tako i kod usvajanja sadržaja nisu dobivene statistički značajne razlike u svim testovima znanja, no i ovdje je vidljiv jasan trend u smjeru boljeg uspjeha kod učenika eksperimentalne skupine u odnosu na kontrolnu skupinu jer u prosjeku učenici eksperimentalne skupine u usporedbi s učenicima kontrolne skupine postižu bolji ukupan rezultat u gotovo svim testovima. Što se tiče veličine efekata, svi dobiveni značajni efekti su veliki što ukazuje na važnost utjecaja igrifikacije u nastavi na usvajanje nastavnog sadržaja iz matematike.
H2: Kvazieksperimentalna i kvazikontrolna skupina ne razlikuju se u razumijevanju znanja nastavnog sadržaja iz matematike
Provedeni t testovi ukazuju na postojanje statistički značajne razlike u razumijevanju nastavnog sadržaja između kontrolne i eksperimentalne skupine kod učenika prvog razreda za prvu (t(39) = −2.67, p < .05, η2=0.155) i drugu nastavnu cjelinu (t(39) = −4.01, p < .05, η2=0.292). Također, značajna razlika između kontrolne i eksperimentalne skupine u razumijevanju nastavnog sadržaja dobivena je kod učenika drugog razreda za prvu nastavnu cjelinu t(41) = −2.24, p < .05, η2=0.109), zatim kod učenika trećeg razreda za prvu nastavnu cjelinu (t(42) = −2.63, p < .05, η2=0.141) te kod učenika četvrtog razreda za prvu nastavnu cjelinu (t(39) = −2.72, p < .05, η2=0.163). Što se tiče smjera dobivenih razlika, pokazalo se da u prvom i drugom razredu sukladno očekivanju učenici eksperimentalne skupine postižu bolji rezultat od učenika kontrolne skupine. Međutim, kod učenika trećeg i četvrtog razreda učenici kontrolne skupine postižu bolji rezultat u razumijevanju nastavnog sadržaja.
Bolje razumijevanje nastavnog sadržaja kod učenika kontrolne skupine u odnosu na eksperimentalnu kod učenika trećeg i četvrtog razreda nije očekivano. Ovakav nalaz teško je objasniti bez prikupljanja dodatnih podataka o učenicima. Moguće je da su neka druga obilježja učenika kao npr. motivacija, inteligencija, samopoštovanje, njihova obilježja osobnosti ili neka obilježja učitelja doprinijela ovakvom rezultatu.
Može se zaključiti da je igrifikacija imala očekivani pozitivan utjecaj na razumijevanje nastavnog sadržaja iz matematike kod učenika prvog i drugog razreda, dok je kod učenika trećeg i četvrtog razreda zabilježen negativan utjecaj igrifikacije.
H3: Kvazieksperimentalna i kvazikontrolna skupina ne razlikuju se u primjeni znanja nastavnog sadržaja iz matematike
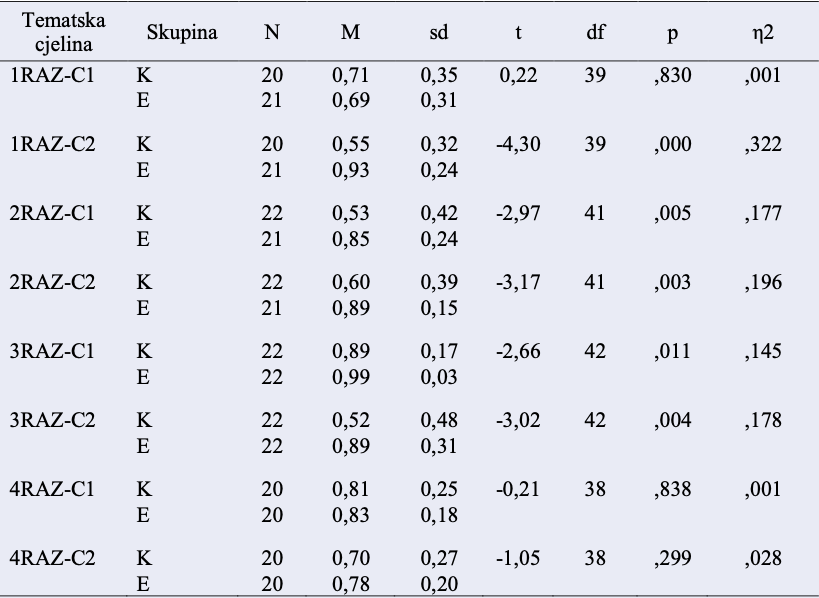
Rezultati t testa pokazuju da postoji statistički značajna razlika u razumijevanju ispitanog nastavnog sadržaja između kontrolne i eksperimentalne skupine u nastavnom sadržaju koje je ispitano u sklopu druge nastavne cjeline u prvom razredu t(39) = −4.30, p < .05, η2=0.322), zatim u razumijevanju prve t(41) = −2.97, p < .05, η2=0.177) i druge (t(39) = −3.17, p < .05, η2=0.196) cjeline kod učenika drugog razreda.
Također, statistički značajna razlika u razumijevanju nastavnog sadržaja između kontrolne i eksperimentalne skupine zabilježena je i kod učenika trećeg razreda i to u prvoj (t (42) = −2.66, p < .05, η2=0.145) i drugoj nastavnoj cjelini t(42) = −3.02, p < .05, η2=0.178. Kod učenika četvrtog razreda nisu dobivene značajne razlike između kontrolne i eksperimentalne skupine. Sve dobivene razlike su sukladno očekivanju, u smjeru boljeg razumijevanja nastavnog sadržaja kod učenika eksperimentalne skupine u odnosu na kontrolnu. Veličine efekta svih dobivenih značajnih razlika smatraju se velikima, što govori o važnosti igrifikacije u nastavi matematike.
Nedostaci i preporuke
U provedenom istraživanju vidljivi su pojedini nedostaci. Prvenstveno je moguć nedostatak odrađenih nastavnih jedinica, ali i mogućnost uvida rezultata kod većeg broja učenika uključenih u istraživanje. To zapravo otvara mogućnost za daljnja istraživanja, posebice kad se radi o primarnom obrazovanju jer je tu provedeno jako mali broj znanstvenih istraživanja. Naravno, to ne isključuje i mogućnost istraživanja kod primjerice studenata.
U buduće istraživanje također bi valjalo uključiti i longitudinalno istraživanje svih navedenih čimbenika. U novom istraživanju valjalo bi uključiti i druge mogućnosti (aplikacije) korištenja u svrhu ostvarivanja nastavnih sadržaja uz pomoć igrifikacije. Na kraju, valjalo bi usporediti slična istraživanja u osnovnim školama u cilju dokazivanja ozbiljnosti razmatranja igrifikacije kao nove nastavne metode.
Zaključak
Veličine efekta svih dobivenih značajnih razlika smatraju se velikima, što govori o važnosti primjene igrifikacije u nastavi. Učenje je cilj koji pokreće društvene djelatnosti. Kako bismo mogli učinkovito učiti, potrebna nam je motivacija i angažiranost (Dichen, 2014). Radi poboljšanja motivacije i angažiranosti učenika u učenju potrebno je da se učitelji nose s brojnim promjenama današnjice, koje nam donosi ubrzani razvoj komunikacijsko-informacijskih tehnologija.
Odgojno-obrazovni stručnjaci moraju biti svjesni da se načini podučavanja mijenjaju. Mijenjaju se generacije, ali i stil učenja. Stoga obrazovni, a posebice stručnjaci za održivi razvoj moraju slijediti trend ili će zaostati, te na taj način smanjiti i stvoriti jednu potpuno neučinkovitu nastavu. U prilog ovoj tezi ide i to što je očigledno da konvencionalne metode podučavanja nisu više toliko zanimljive. Sama ta činjenica ukazuje nam da je i više nego potrebna promjena koja prati trend u podučavanju. Zaista, pomalo je okrutna sama činjenica da se na konvencionalan način podučava čovjek koji je prema prosjeku dvanaest godina igrao računalne igre i videoigre. Način podučavanja treba se približiti takvom čovjeku i pomoći mu u učenju, a ne da mu bude prepreka i novina koja ga sprječava umjesto da mu bude dodatna pomoć u razvijanju svojih potencijala. U prilog tome Kapp (2012.) kaže slijedeće: „ Stručnjaci u odgoju i obrazovanju moraju shvatiti trend rasta korištenja igara čiji se senzibilitet očituje u razvoju nastave kroz stvaranje vremenski utemeljenih aktivnosti, niveliranje iskustvenog učenja, pričanje priča, avatara, ali i drugim tehnikama. Naravno, bodovi i ploče bit će dio toga, ali oni nisu glavni temelj; svi elementi igre moraju biti izvedeni u nastavi inteligentno i pažljivo.“
Odgojno-obrazovni stručnjaci, znanstvenici, profesori i učitelji morat će spajati razne strategije igara sa sadržajem učenja kako bi postigli učinkovite i zadovoljavajuće rezultate. Tu je neizostavno da će se svi morati educirati o tehnikama igrifikacijskog podučavanja kako bi napredovali u podučavanju i zadržali kvalitetu obrazovnog sadržaja i primijenili je u svrhu znanja. Razvojni stručnjaci, profesori i učitelji su zaista u jedinstvenoj poziciji da iskoriste priliku za stvaranje interaktivnih iskustava kod zaposlenika, studenata, učenika ili klijenata koji koriste igrifikaciju.
Tome u prilog idu i rezultati ovog istraživanja koji su pokazali da su sve hipoteze gotovo u potpunosti potvrđene. Potvrđenost se odnosila na pozitivnu korist učinkovitosti i primjene igrifikacije u nastavi primarnog obrazovanja. Na temelju rezultata istraživanja smatramo kako bi se metoda igrifikacije trebala koristiti što više u nastavi primarnog obrazovanja.
Literatura
Baranović, B. (2006). Nacionalni kurikulum za obvezno obrazovanje u Hrvatskoj- različite perspektive. Institut za društvena istraživanja u Zagrebu. Centar za istraživanje i razvoj obrazovanja. Sociologija sela. 44(2/3), 181–200.
Bruner, J. (1976). Nature and Uses of Immaturity, Play Its Role in Development and Evolution. New York: Penguin Books.
Kapp, K. M. (2012). The gamification of learning and instruction: game-based methods and strategies for training and education. United States of America: Pfiffer, A Wiley Imprint
Dichen, C., Dichen, D., Galia, A., i Gennady, A. (2014). From Gamification to Gameful Designand Gameful Experience in Learning. Bulgarian Academy of sciences. Cybernetics and Information technologies, 14(4). Sofia.
Mc Gonigal, J. (2011). Reality Is Broken: Why Games Make Us Better and How They CanChange the World, Penguin Books.
Vygotsky, L. (1978). Mind in society: The development of higher psychological processes Cambridge, MA: Harvard University Press.
Zichermann, G. (2010). Fan is future: Mastering gamification. Google Teach Talk. Dostupno na http://youtu.be/601gNVeaE4g [26.10.2010.]
Zondle. Dostupno na: www.zondle.hr [2.1.2018.]
Aristotel (1992). Politika, Zagreb.
Aristotel (1992). Nikomahova etika, Zagreb.
Comenius, J. A. (1957). Selections: Introduction by Jeana Piageta. Pariz: UNESCO.
Rousseau, J. J. (1989). Emil ili O odgoju. Zagreb: Nakladom hrvatskog pedagoškog zbora
Pinkevich, A. P., Medynsky, E. N., i Pestalozzi, I. G. (1927). Njegov život, podučavanje i utjecaj na rusku pedagogiju
Santos, L. (2012). Friedrich Frobel i njegov pogled na ulogu djetinjstva. Djeca u Europi: zajednička publikacija mreže europskih časopisa, 4(7).
Hrvatska enciklopedija, mrežno izdanje. (2020). Goethe, Johann Wolfgang. Leksikografski zavod Miroslav Krleža. Dostupno na http://www.enciklopedija.hr/Natuknica.aspx?ID=22489 [12.12.2020.]
Hrvatska enciklopedija, mrežno izdanje. (2020). Schiller, Friedrich. Leksikografski zavod Miroslav Krleža. Dostupno na http://www.enciklopedija.hr/Natuknica.aspx?ID=54879
Piaget, J. (1972). Psychology and Epistemology: Towards a Theory of Knowledge. Penguin Books.
2nd International Scientific and Art Faculty of Teacher Education University of Zagreb Conference Contemporary Themes in Education – CTE2 - in memoriam prof. emer. dr. sc. Milan Matijević, Zagreb, Croatia |
Gamification in primary education
Abstract |
|
If you ask students "What is work?" they will answer "school and homework". But if you ask them "What is a game?" they will answer "video games, games on computer, mobile phone, tablet". Clearly, there should be a way to help students learn from what they do best, which is PLAY. This is one of the reasons why gamification is very important in education. In this paper, we will present the history of the use of games and their importance, as well as the importance of gamification in education. We will also present the results of a quasi-experimental study in which the goal was to determine the possibility of applying gamification in mathematics lessons, and to examine the impact of gamification on learning outcomes in the mathematics subject in elementary school.
|
|
Key words |
|
education; game; gamification; primary education; quasi-experimental research; students |